Uno de los problemas típicos en Machine Learning es clasificar los datos de entrada en distintos grupos. Vamos a ver un ejemplo de método de aprendizaje supervisado, donde a partir de un conjunto de datos inicial que pertenece a una categoría conocida entrenaremos un modelo que sepa clasificar datos de los que no disponemos información.
El modelo Support Vector Machine (SVM) es uno de los más utilizados en la actualidad para la toma de decisiones. Los ámbitos en que se utiliza es el diagnóstico de enfermedades (enfermo/sano), clasificación de correos electrónicos (interesante/spam), reconocimiento y clasificación de imágenes, bioinformática, detección de anomalías.
SVM: Aproximación intuitiva
Existen distintas referencias que profundizan en mayor medida en la base matemática del algoritmo. Para comprender cómo funciona desde un punto de vista intuitivo vamos a suponer que trabajamos en un espacio bidimensional, con dos variables X1 y X2.
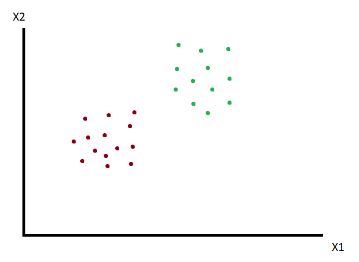
Queremos dividir el conjunto de observaciones en dos clases, rojo y verde. ¿Cómo se podría realizar?
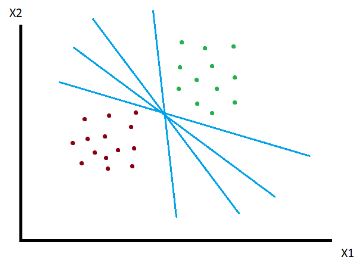
De forma intuitiva podemos ver que existen múltiples rectas que dividen en dos el conjunto de observaciones. Utilizar una u otra tendrá consecuencias respecto a cómo se clasifican las observaciones para las que no disponemos información inicial. Intentar elegir la línea óptima es lo que busca SVM.
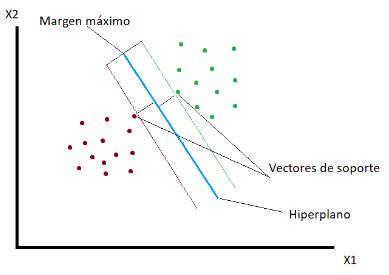
Con SVM la línea se busca a través del margen máximo de los dos puntos más cercanos de la muestra, que se denominan vectores de soporte. Se traza a la misma distancia entre ellos. La suma de las distancias entre ellos debe ser maximizada. Una vez seleccionados, el resto de puntos de la muestra no son significativos para el resultado del mismo.
La línea que divide las clases recibe el nombre de Hiperplano, por la generalización que se hace para espacios multidimensionales.
SVM toma una estrategia diferente a otros algoritmos de clasificación dentro de la familia de MachineLearning. En lugar de centrarse en tomar aquellos elementos más representativos de la muestra y comparar las entradas nuevas con ellos, centra la atención en aquellos elementos que más se parecen y que marcan la diferencia. Se centra en los elementos cuya identificación puede ser más confusa por ser más parecidos entre sí.
Caso de estudio: Clientes potenciales de un nuevo modelo de bicicleta
Para el ejemplo disponemos de un conjunto de observaciones de clientes que han visto el anuncio de un nuevo modelo de bicicleta en redes sociales. Disponemos de un fichero en formato CSV con la edad de la persona que ha visto el anuncio, junto a su salario estimado y si ha comprado o no la bicicleta.
El objetivo es dividir al conjunto de clientes posibles entre aquellos que es posible que compren nuestro producto y los que es menos probable que lo hagan, para tomar decisiones de cara al público objetivo de futuras campañas de marketing.
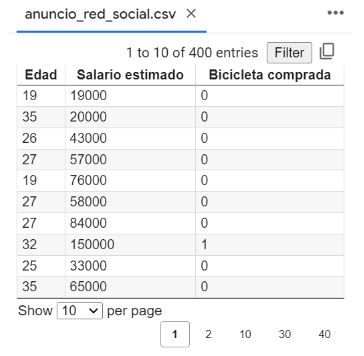
Importar datos y dividir en conjunto de datos de entrenamiento y test
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
dataset = pd.read_csv('anuncio_red_social.csv')
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)Leemos los datos del fichero CSV. En este caso tenemos en X una matriz con las dos columnas correspondientes a las variables de entrada, peso y altura. Dividimos mediante la función train_test_split los datos de entrada entre conjunto de entrenamiento (75%) y conjunto de test (25%). Esto nos servirá para evaluar cómo de bueno es el modelo entrenado sobre datos de los que disponemos.
Feature Scaling
Feature scaling es importante en SVM porque ayuda a que todas las variables de entrada tengan la misma importancia. Esto es clave porque SVM se basa en la distancia entre los puntos de datos. Si las características no están escaladas, los puntos de datos con valores más grandes tendrán una mayor influencia en la ubicación de la frontera de decisión.
En nuestro ejemplo, el salario estimado tiene valores mucho mayores que la edad. Si no aplicamos feature scaling, el modelo le daría mucha más importancia al salario que a la edad.
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
Utilizamos la clase StandadScaller de scikit-learn, con lo que obtenemos una nueva matriz de datos donde tanto salario y como edad están en una escala común.
Entrenando el SVM
from sklearn.svm import SVC
classifier = SVC(kernel = 'linear', random_state = 0)
classifier.fit(X_train, y_train)Utilizamos la clase SVC de la librería para entrenar el modelo, mediante el método fit. Utilizamos los datos de entrenamiento a los que previamente hemos aplicado la técnica de feature scaling. El algoritmo soporta distintos tipos de kernel en función de cómo queremos que se comporte la clasificación de puntos. Esto se indica en la creación del SVC. En nuestro caso elegimos lineal para que la separación sea una línea recta.
Hacer predicciones
Una vez entrenado el modelo podemos hacer predicciones de datos nuevos. Veamos la predicción para una persona que visualiza nuestro anuncio de bicicleta que tiene 25 años y cobra 25.000 euros anuales, va a adquirir el producto.
print(classifier.predict(sc.transform([[25,24000]])))
[0]
El resultado es 0, así que según el modelo SVN la persona no va a comprar la bicicleta que estamos anunciando.
Para hacer la predicción, lo primero que tenemos que hacer es aplicar feature scaling a la entrada, mediante la función transform del StandardScaler que tenemos configurado. Con los datos ya escalados llamamos a la función predict para obtener la predicción.
Utilizamos los datos de prueba para hacer predicciones y compararlas con las salidas esperadas:
y_pred = classifier.predict(X_test);
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))
[0 0]
[0 0]
[1 1]
[1 0]
[0 0]
[0 0]
[0 1]
En la primera línea hacemos las predicciones a partir del conjunto de datos X_test. En la segunda preparamos una matriz donde la primera columna son las predicciones y la segunda son los valores reales. Podríamos examinar la salida para ver los casos en donde el SVM entrenado se equivoca en la predicción, pero sería bastante manual. Por ello veremos a continuación el concepto de matriz de confusión.
Matriz de confusión
La matriz de confusión se utiliza para evaluar el rendimiento de un modelo de clasificación.
from sklearn.metrics import confusion_matrix, accuracy_score
cm = confusion_matrix(y_test, y_pred)
print(cm)
accuracy_score(y_test, y_pred)[[66 2]
[ 8 24]]
0.9
Utilizamos la función confusion_matrix para a partir de los valores reales y_test y los valores predichos con SVM y_pred.
Las filas representan los valores reales para la clasificación, las columnas los valores predichos. En este ejemplo tenemos:
- 66 valores donde la clasificación real es 0 y la predicción es 0.
- 24 valores donde la clasificación real es 1 y la predicción es 0.
- 2 falsos positivos (clasificación real es 0 y predicción es 1).
- 8 falsos negativos (clasificación real es 1 y predicción es 0).
Con accurancy_score obtenemos la precisión del modelo, que en este caso es del 90%.
Visualizar resultados de datos de entrenamiento y prueba
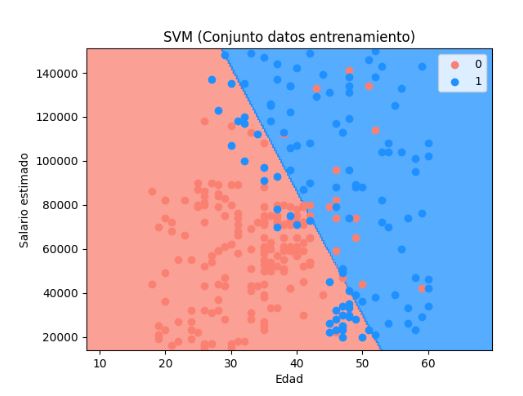
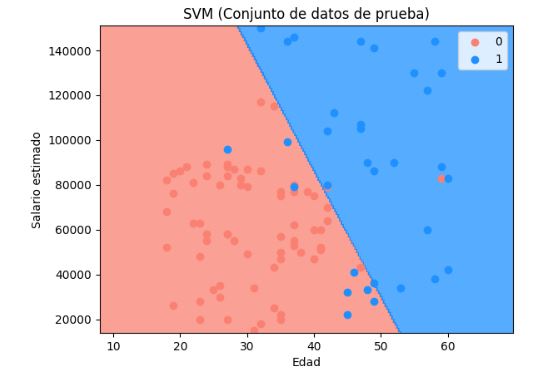
Vemos el hiperplano que divide el espacio de la muestra en dos partes. En azul tenemos el área de los clientes para los que se predice que comprarán el nuevo modelo de bicicleta. En rojo los que la predicción es que no la comprarán. Los puntos en las gráficas son los valores reales de la muestra de datos de entrada.
El ejemplo completo está accesible en Google Colab.



